Bitcoin-Whitepaper阅读笔记

2025-08-14

个人对 Bitcoin-Whitepaper 的一些理解

简介

在互联网贸易中，双方都需要一个值得信任的第三方机构来处理支付，并且完全不可撤销的交易是不存在的（为了解决无法避免的欺诈问题），卖家和买家都互相警惕且要为此付出额外的代价。

比特币的诞生就是为了处理这个问题，我们需要一个基于密码学原理而非信任的电子支付系统，使得双方都能在无信任且无第三方机构的情况下直接进行交易，同时也避免了中心化的第三方机构从中抽成以及该机构权力过大所带来的各种风险，如银行封号，冻结账户等。并且该系统的交易也无法撤销，这将保护卖家不被欺诈，而买家则通过程序化合约保护。

交易

“We define an electronic coin as a chain of digital signatures. Each owner transfers the coin to the next by digitally signing a hash of the previous transaction and the public key of the next owner and adding these to the end of the coin. A payee can verify the signatures to verify the chain of ownership.”

“ 我们将一枚电子货币定义为一条数字签名链。每个拥有者都通过将上一次交易和下一个拥有者的公钥的哈希值的数字签名添加到此货币末尾的方式将这枚货币转移给下一个拥有者。收款人可以通过验证数字签名来证实其为该链的所有者。“

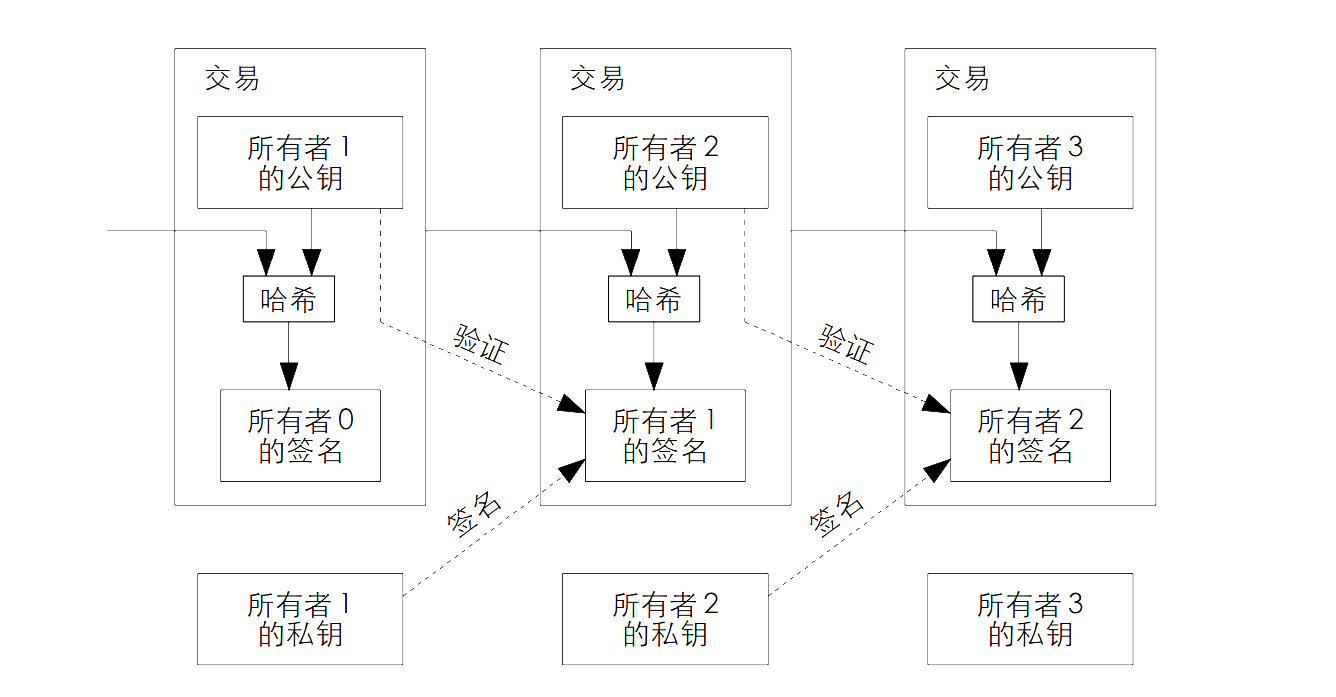这个数字签名链其实就是这个货币的流通过程，完整记录了这枚货币的所有权转移。这串链条完整记录了这枚货币从诞生到每一次交易的全部历史，就像一本公开的 “流转日记”，每一页都是一次交易的签名，环环相扣。

如图，比如所有者1想把该货币转移给所有者2，那么首先1需要将上次的交易详情与2的公钥进行一次哈希计算，得到一个哈希值，再将这个值利用1的私钥进行加密得到1的数字签名，再将签名加入链条的末端，本次交易完成。

2收到这枚货币后用1的公钥解密1添加的那个数字签名，解密成功则说明该签名确实是由1生成（因为1的私钥只有自己知道），之后2可以再次用上次交易详情与自己的公钥进行哈希计算，对比解密值与计算值，若完全一致，则证明没有被修改过。

这个交易的问题是无法判断卖家有没有双重支付，即把一枚货币卖给两个人。我们需要一种能让收款人知道卖方有没有对更早的一笔交易签名的方法，那么在不引入第三方信任机构来鉴定哪笔交易是更先到达的前提下，所有交易就必须公开，由该支付系统所有参与者来共同监督，每笔交易都需要被多数节点认同此次交易是卖家最早的一次签名才算成功完成。

时间戳服务器

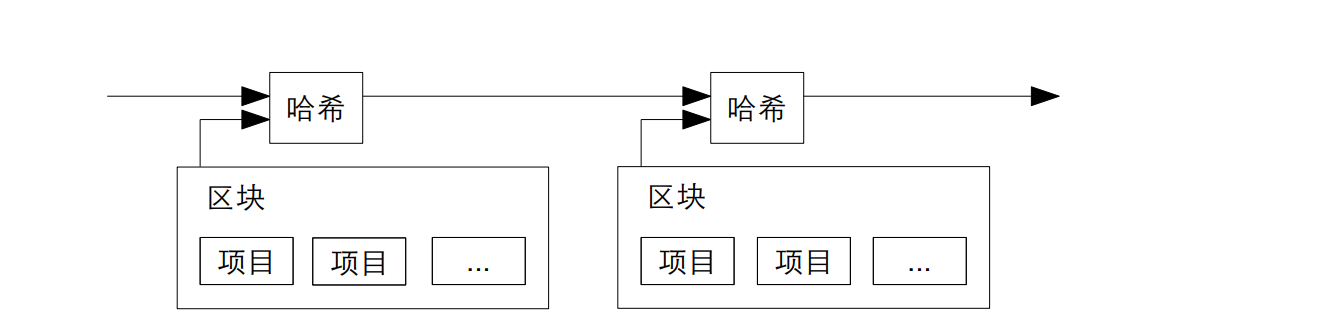
时间戳服务器是防止篡改的核心，服务器会把多个需要记录时间的数据（比如多笔比特币交易）打包成一个 “区块”（可以理解为一个 “数据包”）。然后，用哈希算法（比如 SHA-256）计算这个区块的 “哈希值”。哈希值有个关键特性：如果区块里的任何数据被修改（哪怕一个字符），哈希值会发生巨大变化；反之，只要哈希值不变，就说明区块里的数据完全没被动过。之后会把该哈希值广泛、透明的传播。

该时间戳能证明数据当时一定是存在的，因为时间只要改变了，哈希值就会变。并且后一个区块的哈希值是包含前一个区块的哈希值，若要改变前面区块的信息，那么后面所有区块的哈希值都会改变，又因为所有哈希值都是公开的，所有会被马上发现，这就严格保证了历史区块信息不会被偷偷篡改。

工作量证明

Pow做法是找一个特殊的数（比如 “随机数”），把它和区块数据一起用哈希函数（比如 SHA-256）计算，要求计算结果的二进制开头有 “多个连续的 0”。找到了即可打包区块，接入链中，这就导致了最长的一条链是花费CPU算力最多的，也是最能代表共识的，若要篡改则需要花费大量算力并且超过所有诚实节点的算力。

哈希函数是 “单向的”（从输入算输出容易，从输出反推输入几乎不可能）。要得到 “开头多个 0” 的结果，只能靠不断尝试不同的数去试（类似 “猜密码”），试的次数会随 “0 的数量” 呈指数级增长。而验证很简单，一旦找到这个数，其他人只需把它代入哈希函数重新算一次，看结果是否符合 “开头多 0” 的要求，1 次计算就能验证，不需要重复之前的试错过程。

网络

也就是交易上链的过程。

当有新交易（比如转账、信息记录等）发生时，会向网络中所有节点发送通知；
每个节点会把收到的新交易临时 “打包” 成一个 “区块”（类似快递点把多个包裹打包成一个大包裹）。每个区块里除了交易数据，还包含两个关键信息：上一个区块的哈希值（用来和前一个区块 “链接” 起来，形成链条）；一个待确定的 “随机数”（用于后面的工作量证明）。
开始pow竞争，节点会针对自己打包的区块开始算随机数，本质就是用算力竞争打包权
一旦某个节点完成计算（完成pow证明），就会把这个区块广播给所有节点，宣告 “我打包好了这个区块，大家来验证”。
其他节点收到区块后会进行验证：交易是否合法（比如有没有重复支付、签名是否有效等）；pow证明是否完成。验证通过后节点才会接受这个区块。
接受区块后，节点会把这个区块 “链接” 到自己已有的区块链末尾（用新区块的哈希值作为下一个区块的 “上一个哈希值”），然后继续打包新交易、做新的工作量证明。

网络中可能出现 “同一时间有两个不同区块被广播” 的情况（比如两个节点同时完成工作量证明），这会导致不同节点暂时拥有 “不同的链”。此时规则是：

节点只认 “最长的链” 为正确链。如果自己的链不是最长的，就会切换到最长链上继续工作。
举例：假设 A、B 两个节点同时广播了不同的区块，部分节点先收到 A，部分先收到 B，形成两条分支链。但随着时间推移，其中一条分支会先被延长（比如有节点在 A 的基础上又完成了一个新区块），这条链就成了 “最长链”，所有节点会自动切换到这条链上，另一条分支则被废弃。

这个系统对 “消息丢失” 不敏感，具体体现在：

交易不必传给所有节点：哪怕只有部分节点收到交易，只要这些节点中有一个成功把交易打包进区块并完成工作量证明，交易就会被全网认可（通过区块广播扩散）。
区块丢失可补救：如果某个节点没收到某个区块，当它收到后续区块时，会发现 “上一个区块的哈希值对不上”（中间缺了一环），此时它会主动向其他节点请求丢失的区块，补全自己的链。

激励

即打包奖励，这个过程我们也叫做挖矿。就是上述pow证明竞争的过程，最先完成的节点会获得奖励，即新货币与交易费（一笔交易中的抽成）。

激励机制的核心作用之一是 “让诚实比作弊更有利可图”，从而遏制攻击行为：

假设一个贪心的攻击者掌握了超过全网诚实节点的 CPU 算力（理论上可以篡改区块链），他会面临两个选择：

作弊：篡改交易（比如骗回已支付的货币），但这会破坏整个货币系统的信用，导致他自己持有的货币（包括通过算力生成的）贬值甚至一文不值。
诚实挖矿：继续用算力生成新区块，获取区块奖励和交易费，积累更多有价值的货币。

显然，“诚实挖矿” 的收益远高于 “作弊”，因此攻击者更可能选择遵守规则 —— 这就通过利益驱动保障了系统的安全性。

回收磁盘空间

区块链会不断积累交易数据，如果长期保存所有历史交易，磁盘空间会越来越大。这里提出的解决办法是：

通过 “默克尔树” 结构，只保留关键哈希值，丢弃老交易的详细数据。

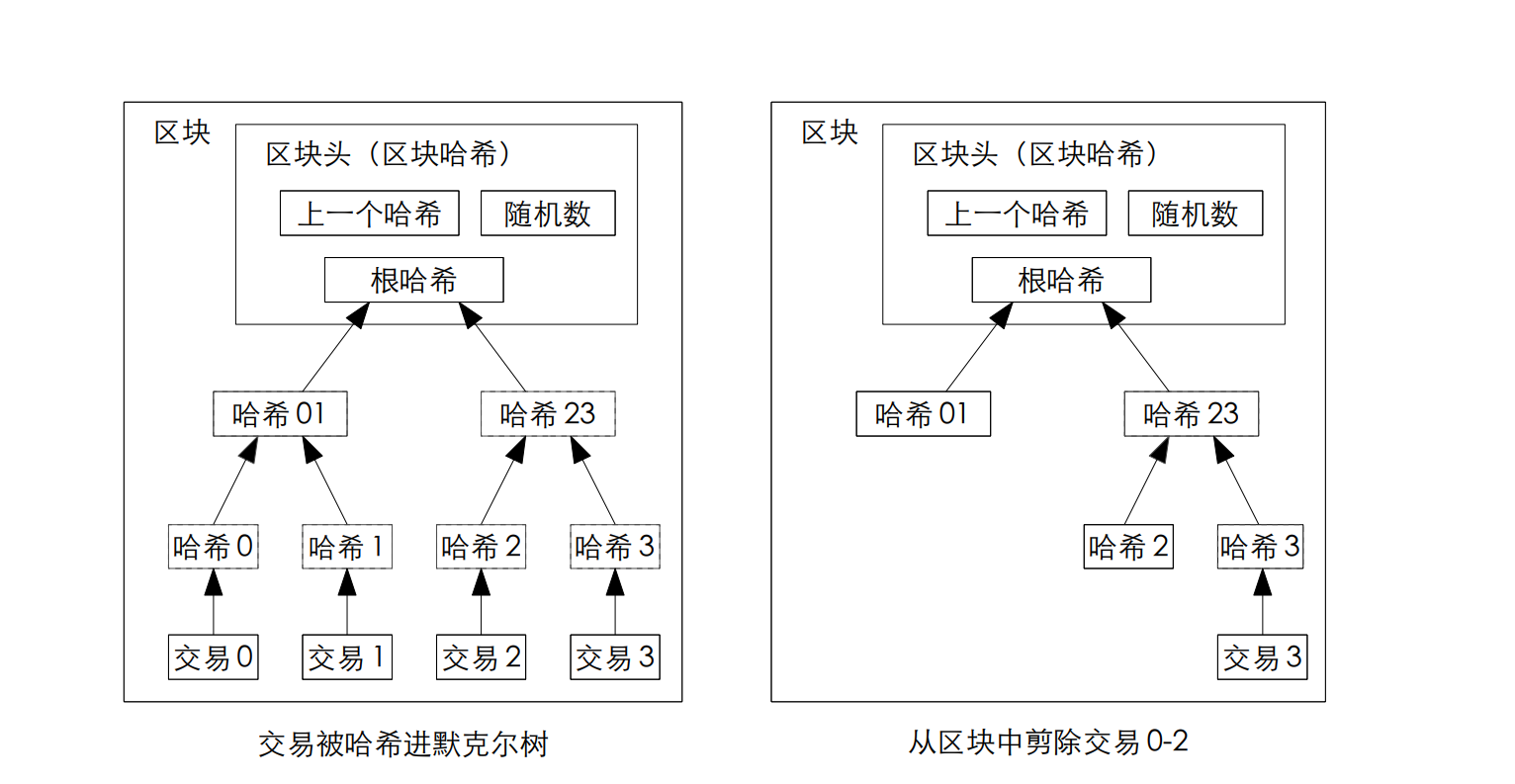
具体做法：所有交易先被 “哈希化”（每个交易生成一个唯一哈希值），再通过默克尔树的结构层层向上哈希（比如两个交易的哈希合并成一个新哈希，再和其他合并哈希继续向上），最终形成一个 “根节点哈希”（默克尔根）。

这个 “默克尔根” 会被写入区块头，成为区块哈希值的一部分。

当一个交易被足够多的后续区块 “覆盖”（即交易已经被全网确认且难以篡改），就可以把这个交易的详细数据删除，只保留默克尔树的根节点和必要的哈希路径。

为什么不影响区块有效性？因为区块的哈希值只依赖默克尔根，而非单个交易的详细数据。即使删除老交易，只要默克尔根不变，区块的哈希值就不变，链的完整性依然成立。

合并和分割交易额

输入：可以是 “一个较大的金额”（来自之前某笔交易的输出），也可以是 “多个较小金额的组合”（来自多笔历史交易的输出）。这些输入的总金额，就是本次交易的 “总支付能力”。

输出：最多包含两个输出： 1. 一个是支付给接收方的金额； 2. 另一个是 “找零”（如果总输入大于支付金额，比如用 100 元付 50 元，剩下的 50 元退还给支付方自己）。

隐私

传统银行的隐私保护靠 “信息封闭”—— 只有银行和交易双方知道交易细节，外人无法访问。但区块链是 “公开账本”，所有交易必须向全网广播（才能被节点验证和记录），因此不能用传统方法，而是换了一种思路：

通过 “公钥匿名” 保护隐私：

区块链上的交易只显示 “公钥地址”（类似一个随机字符串，比如 “1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa”），不直接关联用户的真实姓名、身份证号等信息。公众能看到某地址向另一地址转了多少钱，但无法知道这些地址背后是谁。